A slope is a surface on which one side is up than the other side like a slide and mountain. In mathematics, the slope is used to find the steepness (Height) or path of the line. We can determine the slope of the line by using two points that exist on the line.
In the coordinate plane, the slope is a very useful tool to predict whether the line is parallel or perpendicular to the x-axis or not. In this article, we will discuss the definition of a slope and its types. At last, we will solve some examples.
Definition of the slope
Let (x1, y1) and (x2, y2) be any two Points that exist on the line. Then the ratio between the rate change in y and the rate change in x is called the slope of the line and it is denoted by “m”. Tan θ is equivalent to the slope of the line. Mathematically it is written as
m = tan θ = rate change in y / rate change in x
m = tan θ = Δy / Δx
m = (y2 – y1) / (x2 – x1)
Using the above formula of the slope we can determine the slope of any line by using two given points. We get the point-slope form of the equation after further simplification of the slope formula i.e. m(x2 – y1) = (y2 – y1).
The slope is used to calculate the equation of the straight line i.e. y = mx + b Where b is known as the y-intercept. Slope can also be defined as the ratio between rise and run. Where rise is the change in y and run is the change in x and is written as m = rise/run.
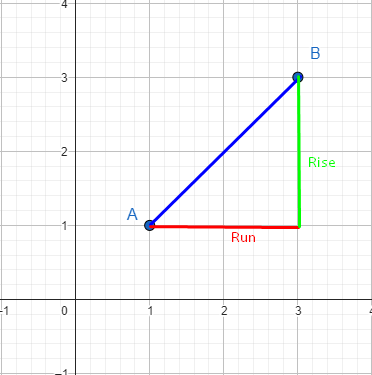
Types of slope
We are going to discuss the 4 different types of slope
- Positive slope
- Negative slope
- Zero slope
- Undefined slope
Positive slope
In a positive slope, the line goes upward from left to right. In other words, the value of y increases by
Increasing the value of x. For example y = 4x – 3, here slope is positive 4 so the line moves upward from left to right.
Negative slope
In a negative slope, the line moves downward from left to right. In other words, you can say the value of y decrease by increasing the value of x. For example, y = – 5x + 4 if you draw the graph then you will observe that the line goes down from left to right.
Zero slope
If the line is parallel to the x-axis it means increasing the value of x but no changes are occurring in y. In this condition, the slope will be zero. You can understand it by using the formula of slope i.e. m = (y2 – y1) / (x2 – x1). Since the rate change in y is zero m = 0 / (x2 – x1) = 0
In this condition the angle with x- axis will be zero or 18o so as slope = m = tan (0) = 0
Undefined slope
If the line is parallel to the y-axis it means the value of y increases but the rate change in x is 0. In this condition, the slope will be undefined. I.e. m = (y2 – y1) / 0 = undefined.
In this condition the angle with x- axis will be 90 so as slope = m = tan (90) = undefined
The slope of the line by using the formula (Example)
We will learn how to calculate the slope of a line by using the slope formula.
Example 1.
Calculate the slope of the line between two points (-1, 1) and (2, 4) also find the angle of the incline
Solution
Step 1: Identify the points x1, x2 and y1, y2. In this example x1 = -1, x2 = 2 andy1 = 1 and y2 = 4
Step 2: Subtract y1 from y2 and subtract x1 from x2. i.e.
Δy = y2 – y1 = 4 – 1 = 3
Δx = x2 – x1 = 2 – (-1) = 2 + 1 = 3
Step 3: Now put the value of Δy and Δx in the formula of slope (m) = Δy / Δx = (y2 – y1) / (x2 – x1). We get
m = 3 / 3
Step 4: After simplifying, we get
m = 1
Step 5: Since tan θ = m, θ = tan-1 (m), as m is equal to 1 so put the value in the formula
θ = tan-1 (1)
θ = 45 Degree
Alternatively, a slope calculator can be used to evaluate the steepness of the line with the help of coordinate points of the line.
Example 2.
Calculate the slope of the line between two points (3, 1) and (2, 4) by graph method.
Solution.
Draw the graph using the given points. Then apply the rise over the run formula of the slope.
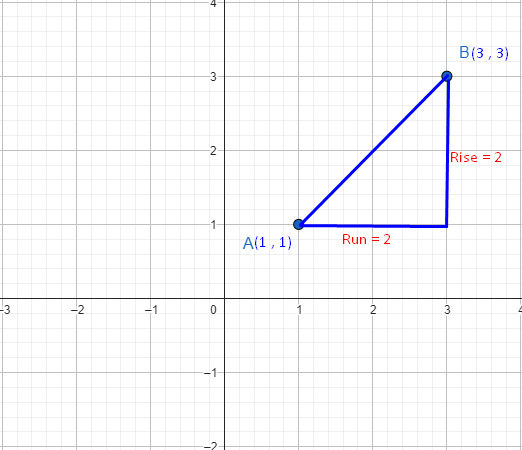
Slope = rise / run = 2 = 2 = 1
Summary
In this article, we have discussed the definition of slope and its mathematical representation in detail. All the terms related to slope are also covered in it. In this article, we discussed two formulas for the slope of the line to find the slope of any between two points. Further, we read the four different types of the slope with examples. We learned two methods to evaluate the slope of the line between two points, one of them is the formula of slope and the other one is a graphical representation. At last we solved some examples by using formula and graphical representations with step-by-step solution. Now you will be able to find slope of any line between two points.
