NCERT Solutions Class 10 Maths Chapter 2 Polynomials Here are the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials to assist students in studying well for their exams. These solutions were created by math topic specialists to help students in getting ready for their board exams. They have formulated these solutions in a way that makes it simpler for students to rehearse the Chapter 2 Polynomials questions using the NCERT solutions. The addition of step-by-step explanations to these Maths NCERT Class 10 Solutions makes learning easier for the students.
Class 10 Maths Chapter 2 Exercise 2.1
1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
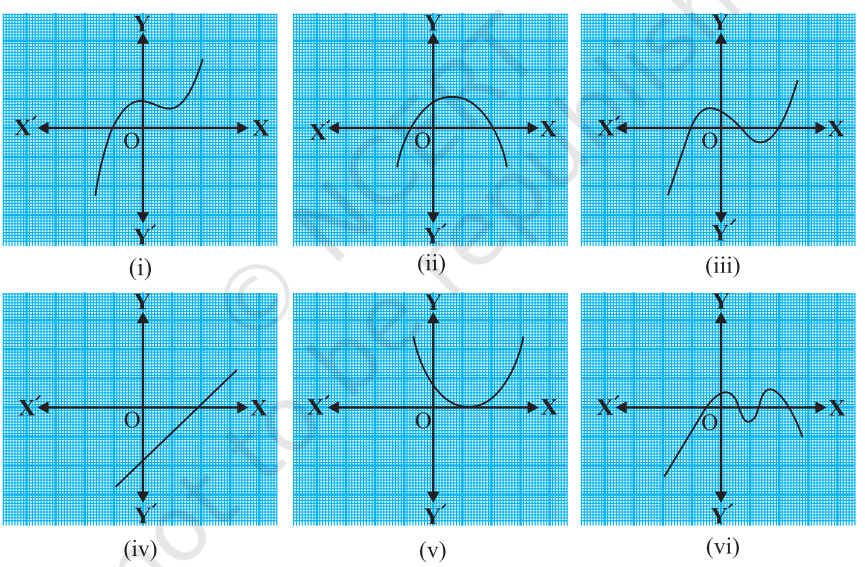
Solution:
Graphical method to find zeroes:-
Total number of zeroes in any polynomial equation = total number of times the curve intersects the x-axis.
(i) In the given graph, the number of zeroes of p(x) is 0
(ii) In the given graph, the number of zeroes of p(x) is 1
(iii) In the given graph, the number of zeroes of p(x) is 3
(iv) In the given graph, the number of zeroes of p(x) is 2
(v) In the given graph, the number of zeroes of p(x) is 4
(vi) In the given graph, the number of zeroes of p(x) is 3
Class 10 Maths Chapter 2 Exercise 2.2
1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2 – 2x – 8 (ii) 4s2 – 4s + 1 (iii) 6x2 – 3 – 7x (iv) 4u2 + 8u (v) t2 – 15 (vi) 3x2 – x – 4
Solution:
(i) x2–2x –8
x2 – 4x + 2x – 8 = 0
x (x – 4) + 2 (x – 4) = 0
(x – 4) (x + 2) = 0
x = 4, x = -2 are the zeroes of the polynomial.
Thus, α = 4, β = -2
Now let’s find the relationship between the zeroes and the coefficients.
For x2 – 2x – 8,
a = 1, b = – 2, c = – 8
Sum of zeroes = – coefficient of x / coefficient of x2
α + β = – b / a
– 2 + 4 = -(-2)/1
2 = 2
Now, Product of zeroes = constant term / coefficient of x2
α × β = c / a
– 2 × 4 = – 8/1
-8 = – 8
Thus, x = 4, -2 are the zeroes of the polynomial.
(ii) 4s2 – 4s + 1
4s2 – 2s – 2s + 1 = 0
2s (2s – 1) – 1 (2s – 1) = 0
(2s – 1)(2s – 1) = 0
s = 1/2, s = 1/2 are the zeroes of the polynomial.
Thus, α = 1/2 and β = 1/2
Now, let’s find the relationship between the zeroes and the coefficients.
For 4s2 – 4s + 1,
a = 4, b = – 4 and c = 1
Sum of zeroes = – coefficient of s / coefficient of s2
α + β = – b/a
1/2 + 1/2 = – (- 4) / 4
1 = 1
Now, Product of zeroes = constant term / coefficient of s2
α × β = c / a
1/2 × 1/2 = 1/4
1/4 =1/4
Thus, s = 1/2, 1/2 are the zeroes of the polynomial.
(iii) 6x2 – 3 – 7x
6x2 – 7x – 3 = 0
6x2 – 9x + 2x – 3 = 0
3x(2x – 3) + 1(2x – 3) = 0
(2x – 3)(3x + 1) = 0
x = 3/2, x = – 1/3 are the zeroes of the polynomial.
Thus, α = 3/2 and β = -1/3
Now, let’s find the relationship between the zeroes and the coefficients:
For 6x2 – 3 – 7x,
a = 6, b = – 7 and c = – 3
Sum of zeroes = – coefficient of x / coefficient of x2
α + β = – b / a
3/2 + (-1/3) = – (-7) / 6
7/6 = 7/6
Now, Product of zeroes = constant term / coefficient of x2
α × β = c / a
3/2 × (- 1/3) = (- 3) / 6
-1/2 = -1/2
Thus, x = 3/2, – 1/3 are the zeroes of the polynomial.
(iv) 4u2 + 8u
4u(u + 2) = 0
u = 0, u = – 2 are the zeroes of the polynomial
Thus, α = 0 and β = – 2
Now, let’s find the relationship between the zeroes and the coefficients
For 4u2 + 8u,
a = 4, b = 8, c = 0
Sum of zeroes = – coefficient of u / coefficient of u2
α + β = – b/a
0 + (- 2) = – (8) / 4
-2 = – 2
Now, Product of zeroes = constant term / coefficient of u2
α × β = c/a
0 × (- 2) = 0 / 4
0 = 0
Thus, u = 0, – 2 are the zeroes of the polynomial.
(v) t2 – 15
t2 – 15 = 0
t2 = 15
t = ±√15
t = -√15, t = √15 are the zeroes of the polynomial.
Thus, α = -√15 and β = √15
Now, let’s find the relationship between the zeroes and the coefficients
For t2 – 15,
a = 1, b = 0, c = -15
Sum of zeroes = – coefficient of t / coefficient of t2
α + β = – b / a
-√15 + √15 = – 0 / 1
0 = 0
Now, Product of zeroes = constant term / coefficient of t2
α × β = c / a
-√15 × √15 = -15 / 1
-15 = -15
Thus, t = -√15, √15 are the zeroes of the polynomial.
(vi) 3x2 – x – 4
3x2 – x – 4 = 0
3x2 – 4x + 3x – 4 = 0
x (3x – 4) + 1(3x – 4) = 0
(x + 1)(3x – 4) = 0
x = – 1, x = 4/3 are the zeroes of the polynomial.
Thus, α = – 1 and β = 4/3
Now, let’s find the relationship between the zeroes and the coefficients
For 3x2 – x – 4,
a = 3, b = – 1, c = – 4
Sum of zeroes = – coefficient of x / coefficient of x2
α + β = – b / a
– 1 + 4/3 = – (-1) / 3
1/3 = 1/3
Now, Product of zeroes = constant term / coefficient of x2
α × β = c/a
– 1 × (4/3) = – 4/3
-4/3 = – 4/3
Thus, x = – 1, 4/3 are the zeroes of the polynomial.
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes, respectively.
(i) 1/4, – 1 (ii) √2, 1/3 (iii) 0, √5 (iv) 1, 1 (v) – 1/4, 1/4 (vi) 4, 1
Solution:
(i) 1/4 , -1
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–(1/4)x +(-1) = 0
4x2–x-4 = 0
Thus, 4x2–x–4 is the quadratic polynomial.
(ii)√2, 1/3
Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2 –(√2)x + (1/3) = 0
3x2-3√2x+1 = 0
Thus, 3x2-3√2x+1 is the quadratic polynomial.
(iii) 0, √5
Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–(0)x +√5= 0
Thus, x2+√5 is the quadratic polynomial.
(iv) 1, 1
Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–x+1 = 0
Thus, x2–x+1 is the quadratic polynomial.
(v) -1/4, 1/4
Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x +αβ = 0
x2–(-1/4)x +(1/4) = 0
4x2+x+1 = 0
Thus, 4x2+x+1 is the quadratic polynomial.
(vi) 4, 1
Sum of zeroes = α+β =4
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2–(α+β)x+αβ = 0
x2–4x+1 = 0
Thus, x2–4x+1 is the quadratic polynomial.
NCERT Solutions Class 10 Maths Chapter 2 Polynomials
The NCERT Solutions for Class 10 Maths are a crucial study tool for students. The Class 10 Math Polynomials NCERT Solutions would assist the students to achieve high scores in the board exams. Additionally, when creating these solutions, professionals concentrated on following the revised CBSE Syllabus for 2023–2024.